Searching and sorting
Objectives
- compare and contrast linear and binary searches
- compare and contrast various sorting algorithms
Searching
Sorting
- we will discuss various sorting algorithms in class
- this is where I draw diagrams on the board and try to illustrate how abstract concepts can be turned into code
- this is also a great opportunity to demonstrate the order of algorithms
- you are not expected to be able to recreate the sorting algorithms out of thin air during the rest of this course,
but hopefully some of the concepts will stick
- you are expected to be able to modify the given sort algorithms to fit new situations you run into - this generally
involves changing the data type used and modifying the comparison code (where it is decided which item comes first)
- the sorts we will hopefully have time to look at:
- bubble sort (n2)
- my sort (n2)
- Wold sort (n2)
- selection (n2)
- insertion sort (n2)
- shell sort (n (log n)2)
- heap sort (n log n)
- quick sort (n log n)
- rob sort (n!)
- Since heapsort and quicksort appear to be tied for the best algorithm, many people
wonder which algorithm is the "best" one to use. In general, heapsort is
safer than a very simple quicksort implementation. Quicksort has a weakness in worst
case situations that take its order to n2. Heapsort doesn't degrade as much
in worst-case scenarios. The weakness in Quicksort is due to the choice of a pivot.
There are quicksort implementations that take this into account and can avoid most worst-case
situations. The structure of quicksort also makes it easy to use other sort routines
to sort subsections of its data, and parallelization shouldn't be too difficult either.
- see Sort2.java for sample sorts with timing information
- Sort.java from CIS 160 is also available
- see DevX.com article on sorting
with Visual Basic code and general commentary
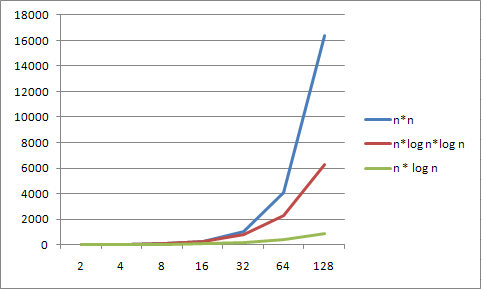
Graphic example of order growth