CIS 260 - Infix tokenizer

The objectives for this assignment are to use associative arrays (HashMaps in this case), a queue, and an extended finite state machine to parse a String containing an arithmetic expression into tokens and place those tokens into a queue for further processing. The next assignment translates the expression from the current infix notation into postfix notation, and then evaluates the postfix expression. Tests should be done to make sure your program works properly before submitting it for grading. Notice that output from a sample run has been provided.

This is a new assignment and it would not be surprising if it contained some errors. Let me know if you find any errors, and I'll be available to check out your code as it develops to help debug it and get it running.

Overview

There are four user-defined classes that make up this assignment.

1. FSM: contains data and methods needed for the finite state machine
2. FSMRule: used internally within the finite state machine
3. Token: represents each token in the input expression
4. Infix: the main program which runs everything

Finite state machines

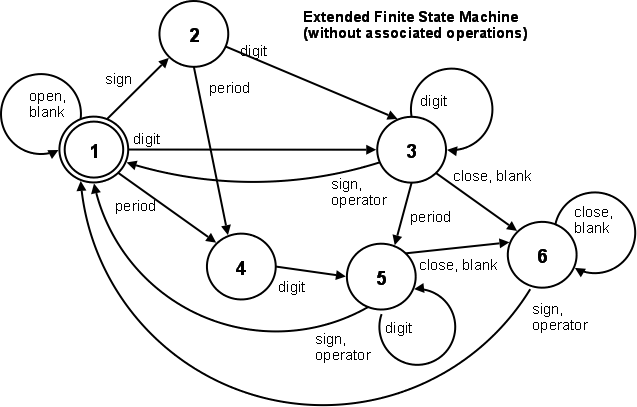
Finite state machines are a concept that is often used in computer programming. You may even have done something equivalent or similar without even realizing it. The basic idea is that there are a finite number of states. You begin in one particular state and start processing input. Each state has rules for what it will do with different types of input. As input is read, the appropriate rule is looked up based on the current state and the input that was read. The rule describes what actions should be taken and the next state to move into. This assignment uses an extended finite state machine (a finite state machine with memory) to parse tokens in an input stream and output them to a queue. The basic diagram for this state machine, without the associated actions, is shown below.

Description of states in state machine

1. waiting for start of operand or open parenthesis
2. operand with sign only so far
3. operand with digits, but no decimal point
4. operand with decimal point, but no digits yet
5. operand with digits and decimal point
6. waiting for operator or close parenthesis

Template

A template is available so you can start with the Token, FSM, and FSMRule classes. It is located at infix.txt.

Infix class

This is the class that you have to write to do all the work. It uses HashMaps, a LinkedList operating as a queue, and implements a finite state machine. There are five static variables and seven static methods.

Note: In the pseudocode below, you may see something like: if rule.actions includes FSM.ERROR. That means that you are actually checking a bit in rule.actions to see if it is set. Fortunately, there are constants already set up in the FSM class to make this easy. Here's the code that would check rule.actions to see if it includes FSM.ERROR:

if ((rule.actions & FSM.ERROR) != 0) { ... }

Infix class static variables/fields

All of the fields should be static and initialized.

• a boolean named DEBUG initialized to false
• a reference variable to hold a new FSM
• a linked list named infixQueue which contains Token objects
• a HashMap named precedences which associates String and Integer objects
• a HashMap named leftAssociative which associates String and Boolean objects

void main(String[] args)

This is the method that does most of the work. It has two main loops, one nested inside the other. The outer loop keeps getting one line of input at a time from the user. The inner loop processes one character at a time from the input data.

1. create a new Scanner object named in
2. call initPrecedences
3. call initAssociativities
4. call initFSM
5. create a boolean named done and set it to false

6. for (String s : args) {
      s = s.toUpperCase();
      if (s.charAt(0) == '-') s = s.substring(1);
      if (s.equals("DEBUG") || s.equals("D")) DEBUG = true;
   }
   System.out.println("Enter an expression to evaluate (or QUIT to exit)");
   if (DEBUG) System.out.println("Program is in DEBUG mode");

7. while not done
   1. create a boolean named error and set it to false
   2. create a variable to hold the state and set it to 1 (the initial state)
   3. create a variable to keep track of the current position and set it to 0
   4. create a variable to count the number of parentheses and set it to 0
   5. create a String variable to hold the operand and set it to be a zero-length String

   6. System.out.print("\nEnter expression: ");
      String expr = in.nextLine().toUpperCase();
      if (expr.equals("QUIT") || expr.equals("Q")) done = true;

   7. clear the infixQueue
   8. while not done and error is false and position is less than expr.length()
   1. create a char named ch to hold the current character and set it; the current character is at position in expr
   2. create a variable to hold an FSM.FSMRule, and set it to the rule obtained using the current state and the current character of input; remember that the finite state machine class has a method for this
   3. if the returned rule is null or rule.actions includes FSM.ERROR, then do the following:

      error = true;
      System.out.println("Error: " + expr);
      System.out.print("       ");
      for (int j=0; j<pos; j++) System.out.print(" ");
      System.out.println("^");

   4. otherwise do the following
      1. if rules.actions includes FSM.APPEND_OPERAND
         • if the length of operand is greater than 0, add a new Token to the end of the infixQueue using: Token.OPERAND, operand, 0, true
         • set operand to a zero length string
      2. if rules.actions includes FSM.CLEAR_OPERAND then set operand to a zero length string
      3. if rules.actions includes FSM.ACCUM_OPERAND then append the current input character to the end of operand
      4. if rules.actions includes FSM.APPEND_OPERATOR
         • get the left associativity of the current character; use left (true) if the leftAssociative HashMap returns null
         • get the precedence of the current character; use 0 if the precedences HashMap returns null
         • add a new Token to the end of the infixQueue using: Token.getType(ch), the current character turned into a String, the precedence, and the left associativity
      5. if rules.actions includes FSM.NONE then do nothing
      6. set the state to whatever rule.nextState is
      7. if the current character is an open parenthesis, add one to the parenthesis counter
      8. if the current character is a close parenthesis, subtract one from the parenthesis counter
      9. if error is false and the parenthesis counter is less than 0 then

         error = true;
         System.out.println("Error: " + expr);
         System.out.print("       ");
         for (int j=0; j<pos; j++) System.out.print(" ");
         System.out.println("^");

   5. if error is false, increment the current position in the input String
   9. if error is false and the parenthesis counter is not 0 then

      error = true;
      System.out.println("Error: " + expr);
      System.out.print("       ");
      for (int j=0; j<pos; j++) System.out.print(" ");
      System.out.println("^");

   10. if done or error is true, then continue (do next iteration of loop)
   11. if the operand length is greater than 0, then add the operand as a new Token to the end of the infixQueue using: Token.OPERAND, operand, 0,true
   12. if DEBUG is true

       System.out.println("Infix queue:");
       for (int i=0; i<infixQueue.size(); i++) System.out.printf("%2d: %s\n", (i+1), infixQueue.get(i));

boolean isLeftAssociative(String operator)

This is a pretty simple static method whose job is to return true if an operator is left associative, and false if it isn't. The associativities are already stored in the leftAssociative HashMap, which makes this routine rather short.

• use the operator passed in to get the Boolean value associated with it from the leftAssociative HashMap
• if the value returned was null, then return true
• if the value returned was not null, return it

int getPrecedence(String operator)

This is a pretty simple static method whose job is to return the integer precedence value of an operator. The precedences are already stored in the precedences HashMap, which makes this routine rather short.

• use the operator passed in to get the Integer value associated with it from the precedences HashMap
• if the value returned was null, then return 0
• if the value returned was not null, return it

void initPrecedences()

This is a pretty straight-forward method. It is a static method which adds the associations in the following list into the precedences HashMap.

• "-", 1
• "+", 1
• "*", 2
• "/", 2
• "%", 2
• "^", 3

void initAssociativities()

This is a pretty straight-forward method. It is a static method which adds the associations in the following list into the leftAssociative HashMap.

• "-", true
• "+", true
• "*", true
• "/", true
• "%", true
• "^", false

void errorExit(String msg)

This method is simple. Print "Error: " followed by the msg passed in. Then end the program.

void initFSM()

A static method named initFSM. It should add the rules in the list below to the finite state machine. The rules in the list below are in the following format: state, character type, actions, next state. Check out the FSM class for the appropriate method to be used to enter a rule into the finite state machine. You should already have a reference variable to a FSM.

• 1, FSM.SIGN, FSM.ACCUM_OPERAND, 2
• 1, FSM.DIGIT, FSM.ACCUM_OPERAND, 3
• 1, FSM.PERIOD, FSM.ACCUM_OPERAND, 4
• 1, FSM.OPEN, FSM.APPEND_OPERATOR, 1
• 1, FSM.BLANK, FSM.NONE, 1
• 2, FSM.DIGIT, FSM.ACCUM_OPERAND, 3
• 2, FSM.PERIOD, FSM.ACCUM_OPERAND, 4
• 3, FSM.SIGN, FSM.APPEND_OPERAND | FSM.APPEND_OPERATOR, 1
• 3, FSM.DIGIT, FSM.ACCUM_OPERAND, 3
• 3, FSM.PERIOD, FSM.ACCUM_OPERAND, 5
• 3, FSM.CLOSE, FSM.APPEND_OPERAND | FSM.APPEND_OPERATOR, 6
• 3, FSM.OPERATOR, FSM.APPEND_OPERAND | FSM.APPEND_OPERATOR, 1
• 3, FSM.BLANK, FSM.APPEND_OPERAND, 6
• 4, FSM.DIGIT, FSM.ACCUM_OPERAND, 5
• 5, FSM.SIGN, FSM.APPEND_OPERAND | FSM.APPEND_OPERATOR, 1
• 5, FSM.DIGIT, FSM.ACCUM_OPERAND, 5
• 5, FSM.CLOSE, FSM.APPEND_OPERAND | FSM.APPEND_OPERATOR, 6
• 5, FSM.OPERATOR, FSM.APPEND_OPERAND | FSM.APPEND_OPERATOR, 1
• 5, FSM.BLANK, FSM.APPEND_OPERAND, 6
• 6, FSM.SIGN, FSM.APPEND_OPERATOR, 1
• 6, FSM.CLOSE, FSM.APPEND_OPERATOR, 6
• 6, FSM.OPERATOR, FSM.APPEND_OPERATOR, 1
• 6, FSM.BLANK, FSM.NONE, 6

Sample run

C:\>java Infix
Enter an expression to evaluate (or QUIT to exit)
Program is in DEBUG mode

Enter expression: (5+2) * (.3 - -3.3)
Infix queue:
 1: open parenthesis
 2: operand (5)
 3: operator (+), 1, true
 4: operand (2)
 5: close parenthesis
 6: operator (*), 2, true
 7: open parenthesis
 8: operand (.3)
 9: operator (-), 1, true
10: operand (-3.3)
11: close parenthesis

Enter expression: ( 6     + 2.3)  ) -1
Error: ( 6     + 2.3)  ) -1
                       ^

Enter expression: ( 6     + 2.3)   -1
Infix queue:
 1: open parenthesis
 2: operand (6)
 3: operator (+), 1, true
 4: operand (2.3)
 5: close parenthesis
 6: operator (-), 1, true
 7: operand (1)

Enter expression: 3 +-.78*((2++14.9   * 3.)^(3+(2*5)))
Infix queue:
 1: operand (3)
 2: operator (+), 1, true
 3: operand (-.78)
 4: operator (*), 2, true
 5: open parenthesis
 6: open parenthesis
 7: operand (2)
 8: operator (+), 1, true
 9: operand (+14.9)
10: operator (*), 2, true
11: operand (3.)
12: close parenthesis
13: operator (^), 3, false
14: open parenthesis
15: operand (3)
16: operator (+), 1, true
17: open parenthesis
18: operand (2)
19: operator (*), 2, true
20: operand (5)
21: close parenthesis
22: close parenthesis
23: close parenthesis

Enter expression: 7.8 + -3.0001
Infix queue:
 1: operand (7.8)
 2: operator (+), 1, true
 3: operand (-3.0001)

Enter expression: quit

C:\>