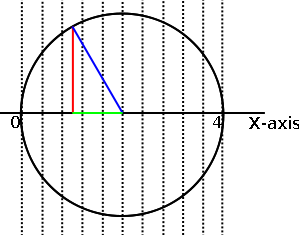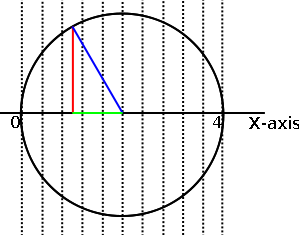CIS 260 - Volume Calculator
The objectives of this assignment are:
- create and use methods
- validate user input
- format output using System.out.printf or String.format
Overview
You have to write a program that will calculate the volume of a solid
by dividing the object into rough slices and sum up the volume of the
individual slices. The program has to run the calculation several
times using more and more slices to try to get more accurate volume
estimates. User input must be validated and output must be formatted
to match the example given below. Your program has to have the methods
described in the requirements section.
Check out http://ceemrr.com/Geometry2/Sphere/Sphere2.html for
a graphic example of slicing a sphere to calculate its volume.
Requirements
- Create a method named getDouble which takes three arguments:
a String prompt, a double minimum value, and a double maximum value. The prompt
should be displayed before getting a string as user input. That string should
then be checked to see if it represents a valid floating point number. If it does,
then it should be checked to make sure it is between the minimum and maximum values.
If there are any errors, an appropriate error message should be displayed and the
user should be prompted to re-enter a value. If there are no errors, then the double
value of the entered string should be returned. You can use a data input and
validation method discussed in class if you wish as long as it works properly.
- Create a method named getVolume which takes three arguments:
a double minimum value, a double maximum value, and an integer number of slices.
This method is used to slice up the object being measured and add up the
volumes of the slices. The object is assumed to be aligned along the x-axis. The
minimum and maximum values represent the range on the x-axis over which we will
be calculating the volume of the object.
- Calculate the width of each slice. The width of each slice is equal to
the difference between the maximum and minimum values divided by the
number of slices.
- For each slice, you will need to calculate the x-axis coordinate
of the slice. Slice 0 starts at the minimum value. Slice 1 starts at
the minimum value plus the width of one slice. Slice 2 starts at
the minimum value plus two times the width of one slice. Once you know
where a slice starts, add half the width of a slice to the x coordinate
so you are getting the area at the midpoint of that slice.
- Sum up the volume of each slice of the object. The volume for each slice
can be obtained by multiplying the width of a slice times its area.
The area of a slice can be obtained by calling the
getSliceArea method. You must send the
getSliceArea method the x coordinate for the slice
you want the area of.
- Create a method named getSliceArea which takes one argument:
a double x-coordinate value. This method will change depending on the type of
object you want to calculate the volume of. The steps below refer to calculating
the volume of a sphere of radius 1 with its origin at 1 on the x axis. This is
the solid you should be calculating the volume of with your program.
- If x is outside of the range of the sphere, which is 0 to 2 in this
case, then return 0 (since there is no area to calculate).
- Each slice is a circle. You need to get the radius of that circle to
calculate the area of the slice. You can use the Pythagorean theorem
to get the radius of the slice. The radius is the opposite side of a
triangle formed by the origin of the sphere, the x-axis coordinate for
the slice, and a point on the surface of the sphere directly above the
x-axis coordinate. In this case, the adjacent side has a length equal
to the x axis coordinate subtracted from the origin's x coordinate.
The hypotenuse length is equal to the sphere's radius. Given that, the
radius of the slice is the square root of the square of the hypotenuse
minus the square of the adjacent side. The area is then Pi times the
radius squared.
- The main method will display eleven calculations for the volume using
increasingly larger numbers of slices. Increasing the number of slices will
usually increase the precision of the volume calculation.
- Ask the user for minimum and maximum x-axis values. These represent the
range over which the volume will be calculated. You must include error
checking to make sure the user enters valid numbers.
- Display headings for the report. See the sample output for the format.
- Create a loop for the number of slices to process, starting with 1 and
doubling each iteration: 1, 2, 4, 8, ..., 1024
- For each number of slices, display the number of slices and the
calculated volume using the exact format shown in the example output.
For example, the number of slices should be in a column with a width of six.
The volume should be in a column with a width of ten characters and
display five digits sfter the decimal point.
- You can get the volume by calling getVolume and sending
it the minimum and maximum x-axis values and the number of slices.
Example
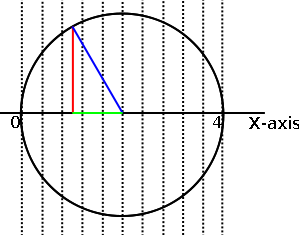
The diagram above is a side view of a sphere with a radius of 2 centered
at 2 on the x-axis. The dotted lines show how the sphere is divided into ten
equal width slices. The blue, red and green lines show a triangle used to help
calculate the volume of the third slice from the left.
In this case, since the diameter of the sphere is 4 and there are 10 slices,
the width of each slice is 4/10. The third slice starts at .4 times 2 on the
x-axis. The midpoint of the slice on the x-axis is an additional half-width
of a slice. That puts the midpoint at 1.0 on the x-axis. That is the point at
which the red line intersects the x-axis in the diagram.
The length of the green line is the radius of the sphere minus the midpoint
of the slice. This ends up also being 1.0 in this case since 2 - 1 is 1.
The length of the red line can be determined using the Pythagorean theorem.
The length of the blue line is the square root of the sum of the squares of
the lengths of the red and green lines. Therefore, the length of the red line
is the square root of the blue line squared minus the green line squared.
Once we know the length of the red line, then calculating the volume of the
slice is easy. We are doing a rough approximation assuming the slice is a
disc. This ignores the curve at the outer surface of the sphere, but as we
make the slices thinner, our approximations become more precise. The volume
is the width of the slice multiplied by Pi multiplied by the radius squared.
We know the width of the slice, Pi is a constant, and the radius is the length
of the red line.
If we do that for each slice and sum the results, we get an approximate
volume for the whole sphere.
Special notes
- We may develop a data input method similar to getDouble in class.
- Pi is available in Java as: Math.PI
- You can get the square root of x in Java using: Math.sqrt(x)
Grading rubric
Note: Program must be able to be compiled and run to get any points.
- 5 pts: style conventions followed (no tabs, proper indentation, documentation comments)
- 5 pts: double getDouble(String, double, double) method works properly
- 10 pts: double getSliceArea(double) method works properly
- 15 pts: double getVolume(double, double, int) method works properly
- 10 pts: void main(String[]) method works properly
- 5 pts: output formatting matches sample
Sample output
Enter minimum x: 0
Enter maximum x: 2
Slices Volume
------ ----------
1 6.28319
2 4.71239
4 4.31969
8 4.22152
16 4.19697
32 4.19084
64 4.18930
128 4.18892
256 4.18882
512 4.18880
1024 4.18879